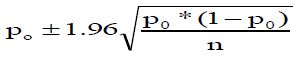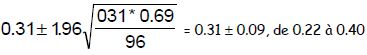2
.
3
-
Les données par rapport à la réalité
La description d’un échantillon est toujours un peu fausse par rapport à la situation de toute la population d’où est extraite l’échantillon. Le hasard a pu faire en sorte que la moyenne, ou le pourcentage trouvé ne sont pas exactement ceux de la population.
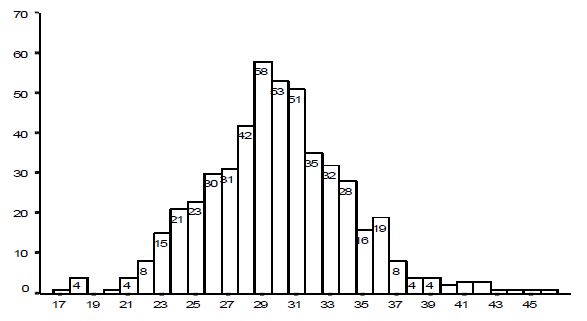
Exemple : dans une urne remplie de boules, on dispose de 31 % de boules rouges (taux dit théorique ou taux vrai). Si je prend 96 boules en tout, combien de boules rouges vais-je trouver ? EN MOYENNE, je vais en trouver 31 % * 96 = 30 boules rouges. Mais je pourrais en trouver 29, 32, 50, ou 0, ou 100 ! Tout est possible, mais tout n’est pas également probable. Un calcul simple permet de dire que j’ai 95 % de chances de tomber entre 21 et 39 boules. Cela veut dire que, en clinique habituelle, je sonde une urne théorique (les femmes enceintes, les femmes en suite de couches...) dont j’ignore la composition, et le hasard va me faire osciller pour un taux observé entre 22 % et 40 % dans 95 % des cas, et en dehors dans 5 % des cas !
De la même manière, dans une situation clinique habituelle, un pourcentage observé n’est que le reflet approximatif du taux vrai. Pour calculer le taux vrai probable, il suffit d’affecter au taux observé po une fourchette dans laquelle se situe raisonnablement ce taux vrai (95 % de chances) :
La formule est la suivante :
avec po le pourcentage, et n le nombre d’observations. Plus il y a d’observations, plus la fourchette est étroite +++.
Donc, dans des résultats d'enquêtes, c'est un gage de sérieux que de donner le nombre total d'observations sur lesquelles le pourcentage est calculé, et de présenter l'intervalle de confiance du pourcentage à 95 %.
Exemple : taux d'infections nosocomiales à Rotavirus dans les services de Pédiatrie sur 9 hôpitaux sur 5783 entrées : 3.9 % (IC à 95 % : 3.4 - 4.5 %)
Pour les données quantitatives, le raisonnement est le même : on démontre que l’on a 95 % de chances que la moyenne vraie se situe entre + 1.96 σ et - 1.96 σ.
Nombre de boules moyen : 31 % de 96 boules = 30
Calcul de l’intervalle de confiance à 95 % :
= du pourcentage :
= du nombre de boules : sur 96 boules, soit 21 à 39
Nombre de tirages théoriques hors de l’intervalle de confiance à 95 % : 5 % du nombre de tirages, soit 25.
Nombre observé : 22
2
.
4
-
Croisement des données. Comparaisons.
Comparer, c’est faire des mesures avec le même instrument dans deux groupes de patients ou dans deux situations : comment procéder ? L’intuition est mauvaise conseillère : si on trouve 2 % dans un cas et 4 % dans un autre, peut-on dire que c’est le double, comme dans 30 % et 60 % ?
2
.
4
.
1
-
Principe des tests
Un test statistique permet de répondre à la question. Il n’est pas nécessaire d’en connaître les calculs, mais de savoir lesquels utiliser et sous quelles conditions. Les logiciels bien faits aident à comprendre les tests. Quelques noms :
- Pour les pourcentages (deux variables qualitatives) : test du Χ² (chi-deux), test de Fisher,
- Pour les moyennes ou les médianes (une variable quantitative et une variable qualitative) : test t de Student pour deux moyennes, et analyse de variance pour plus de deux moyennes. En cas de petits effectifs, utiliser le test de Wilcoxon (idem Mann-Whitney) pour deux moyennes, et de Kruskall-Wallis pour plus de deux moyennes.
- Pour deux variables quantitatives : coefficient de corrélation, droite de régression.
2
.
4
.
2
-
Comparaison de (2 ou plus) pourcentages
Comment dire que 2 pourcentages sont différents ? Peut-on dire 'intuitivement' que 10 % est différent de 11 %, de 12 %, de 20 % ? A-t-on le droit de dire que 6 % (ou 40 %) est le double de 3 % (ou 20 %) et à ce titre que ces 2 pourcentages sont différents ? Ou que 30 % est différent de 40 % parce que il y a 10 % en plus ?
On voit à la lumière de l’intervalle de confiance que 31 % sur 100 boules est équivalent (au sens statistique) à 39 % ou à 22 %. On dira que, sur 100 boules, 31 % et 39 % sont semblables, mais que 40, 41, ou 42 % est sans doute différent (c'est-à-dire que 40 % sort de l'intervalle de confiance de 95 %, ou que 40 % est différent au risque de 5 % ==> c'est le sens de p < 0.05). A contrario, si les pourcentages peuvent venir de la même urne, on ne peut pas prouver que les pourcentages sont différents.
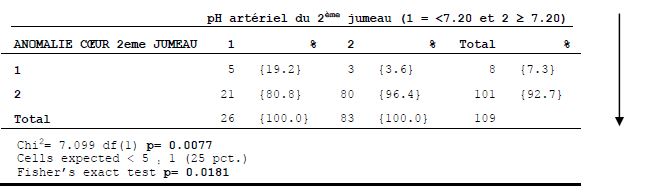
Le test pour comparer deux pourcentages (ou plus) est le X² (chi-deux, ou chi-carré), ou le test de Fisher en cas de petits effectifs. A l'aide d'une formule, ou d'un programme statistique, on conclue par ce test que les pourcentages sont différents au risque de 5 %. Le nombre d'observations compte : plus vous avez de sujets, plus l'intervalle est étroit.
Exemple de sortie EPIDATA avec la commande (voir infra) : tables ph2c arcf2 /c /t /ex /sa
2
.
4
.
3
-
Comparaison de deux moyennes
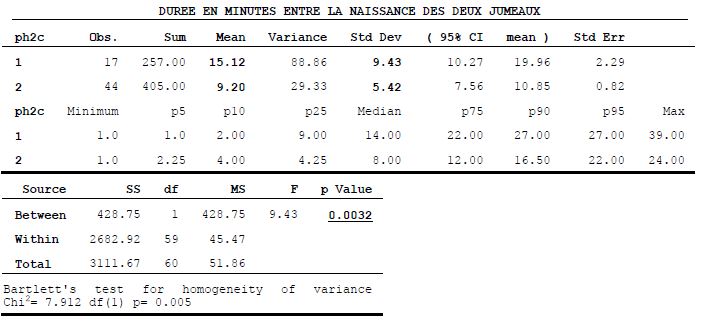
Le test utilisé est le test t de Student. L’hypothèse nulle est que les deux moyennes se ressemblent. Le test tient compte de l’écart entre les deux moyennes, rapporté aux écarts-types des deux moyennes. Le raisonnement est le même que celui des pourcentages : si l’écart est grand, on peut penser que les moyennes viennent de deux échantillons différents, au risque de 5 %. Si l’écart est petit, on ne peut pas montrer que les moyennes diffèrent. La comparaison de plusieurs moyennes est assez complexe : ANOVA (analysis of variance).
Exemple de commandes avec EPIDATA : means duree ph2c /t
2
.
4
.
4
-
Corrélation et régression
Lorsque l'on veut comparer deux séries de données quantitatives (poids de naissance et âge de la mère, glycémies avant et après, données de laboratoires....), on peut utiliser :
-
la régression : construction d'une courbe et de son équation (régression linéaire si la courbe est une droite, avec la pente de la droite). Exemple : peak-flow et taille des enfants dans une enquête en milieu scolaire : Peak = 5 x taille (en cm) - 421
-
la corrélation avec un coefficient r qui varie de -1 à +1, avec un degré de signification attaché au résultat. Dans la même enquête, r = 0.69 (p très significatif)
- Durée de vie, Courbe de survie : courbe actuarielle à espaces libres, courbe de Kaplan-Meier ou courbe actuarielle à espaces fixes
2
.
5
-
Le raisonnement statistique
2
.
5
.
1
-
Résultats d’un test de comparaison
le test est dit significatif si p < 0.05 : cela veut dire que les pourcentages ou les moyennes étudiés sont statistiquement différents ou que la différence n’est pas due au hasard (en ayant un petit risque de se tromper, ici moins de 5 % de risque de se tromper, c’est ce que veut dire le « p »).
le test est dit non significatif – c’est-à-dire que l’on ne peut pas conclure – si p ≥ 0.05 : cela veut dire que la différence entre les pourcentages ou les moyennes peut être due au hasard, ou que le risque de se tromper en disant qu’il y a une différence est trop grand, ou, dans le doute, on préfère ne pas conclure.
2
.
5
.
2
-
Deux risques d’erreur dans le raisonnement (à propos de comparaison de deux traitements) :
- conclure que les traitements sont différents, alors qu’ils sont semblables. Ce risque d’erreur est connu quand on conclue à une différence significative et consenti : il est de 5 % et il est dit de première espèce. Il est dû à la fluctuation des % ou des moyennes dans un échantillon.
- conclure que les traitements sont semblables, alors qu’ils sont différents. En fait, lorsque la différence n’est pas significative, on ne conclue pas que les traitements sont semblables, on préfère ne pas conclure, ou dire qu’on ne peut pas mettre en évidence de différence. En effet, il peut y avoir une différence qu’on ne peut mettre en évidence avec l’expérience utilisée (risque de deuxième espèce). Le facteur le plus habituel est le manque de sujets : s’il existe une différence et que le nombre de sujets est faible, on risque de ne pouvoir trouver cette différence.
3/12