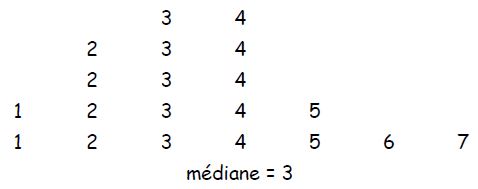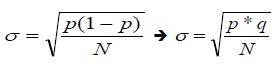2
-
Analyse des données, Statistique
2
.
1
-
La mesure : quelle est la valeur de l’instrument ?
Une mesure se fait avec un instrument comme le « mètre » ou la toise pour la taille ou le PC, l’échographe pour la clarté nucale, la balance pour le poids, la prise de sang pour le triple test… Cet instrument doit avoir les caractéristiques suivantes :
-
Validité : l’instrument doit mesurer ce qui doit être mesuré. Exemple : la mesure de l’obésité ne se fait pas par le poids, mais le rapport P/T² qui est l’indice de masse corporelle avec les limites pour l’adulte de 25 (surpoids) et de 30 (obésité). Deux situations où la validité se pose : (1) il existe un « gold standard » (IMC, douleur, durée du travail en cm/h), (2) il n’existe pas de mesure consensuelle (satisfaction lors de l’accouchement, importance des contractions, monitoring foetal, MAP..) : pouvoir valider la mesure que l’on utilise.
-
Pertinence clinique : score de gravité des patients (état clinique), vitalité et monitoring foetal ou auscultation. Exemple de mesure non pertinente : faire coder la douleur ou la satisfaction des patients par un médecin, au lieu de le faire par les patients eux-mêmes.
-
Simplicité : faisabilité, acceptabilité, coût, technicité, temps de mesure. Exemple d’absence de technique : les échelles visuelles analogiques.
-
Exactitude : mesure exactement ce qu’il est censé mesurer.
-
Précision : mesure sans dispersion.
-
Reproductibilité ou fiabilité ou fidélité (reliability) : c’est une grande difficulté. Il peut exister plusieurs difficultés :
- la variabilité intra-obervateur : l’observateur ne va pas, tout au long des interrogatoires, coder de la même manière,
- la variabilité inter-observateur : les différents observateurs ne vont pas coder de la même manière.
D’où la nécessité de bien définir des items choisis, de réunir des observateurs pour leur préciser les définitions. Taux de concordance
-
Sensibilité et spécificité, capacité discriminante : le critère sépare bien les malades des nonmalades.
Choix du niveau de seuil. Exemple : la glycémie dans le diabète gestationnel, la longueur du fémur dans les RCIU, les tests sanguins pour la trisomie 21.
→ Exemple de mesures à commenter (à éviter dans les essais actuellement) : dilatations du col, les contractions, les chiffres de tension artérielle, le repos, une hospitalisation (de jour, de nuit...), une durée d’hospitalisation, un diabète gestationnel, un tabagisme (combien de cigarettes/jour), une grossesse normale, un bassin étroit, une stagnation de la progression foetale, une durée d’accouchement, menace d’accouchement prématuré, douleur du nouveau-né…
2
.
2
-
Description
2
.
2
.
1
-
Les données sont quantitatives (continues)
2
.
2
.
1
.
1
-
Valeur centrale
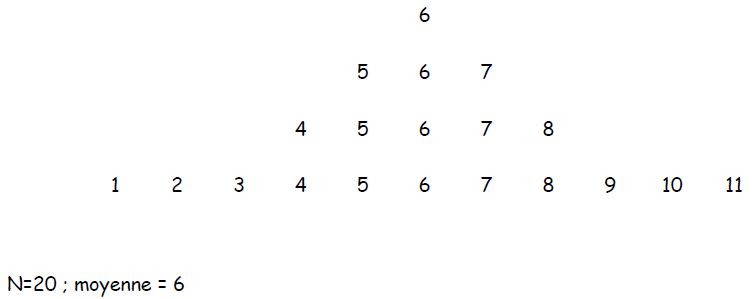
→ La répartition est symétrique :
moyenne :
→ La répartition est asymétrique et les données sont peu nombreuses :
* médiane : valeur telle que 50 % des valeurs soient au-dessus, et 50 % au-dessous. C’est une valeur de rang.
- Nombre de valeurs impaires : 12 15 19
20 23
- idem : 12 15
19
20 56
- Nombre de valeurs paires : 12 15
16 18
20 29 => médiane = 17
* analyse par groupes ou transformation en classes
2
.
2
.
1
.
2
-
Valeurs de dispersion
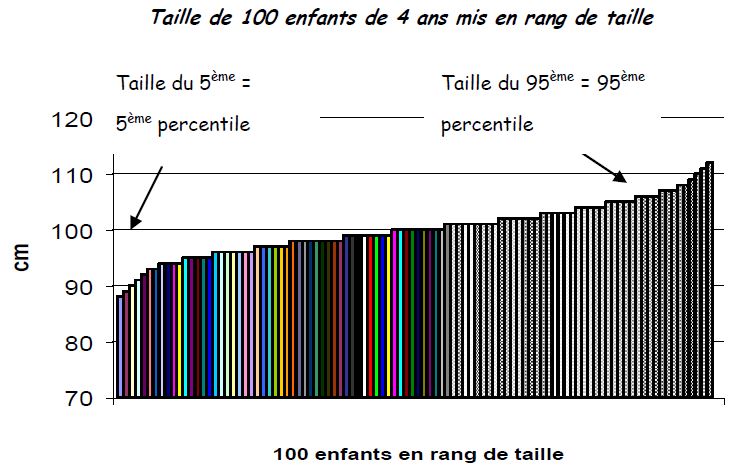
* percentiles, quartiles... : valeur de rang, c’est-à-dire valeur prise par une mesure dans une série rangée dans un ordre croissant. Le 10ème percentile sur 100 est la valeur de la mesure du sujet rangé en 10ème. Idem pour le 90ème ou le 97ème, ou le 3ème. Premier quartile (Q1) : 25ème percentile ; troisième quartile (Q2) : 75ème percentile. Deuxième quartile : médiane. Notion de valeur « normale » ou « anormale » : 10ème, 3ème ?
* écart-type (déviation standard) : moyenne des écarts à la moyenne
Exemple : population A. n=20 ; m = 6 ; variance = 122/19 = 6.4 ; écart-type = 2.5
Exemple : population B. n=20 ; m = 6 ; variance = 2.9 ; écart-type = 1.7
* Les liens entre percentiles et écart-type
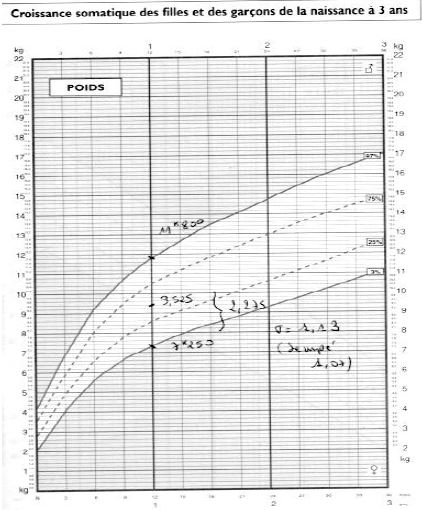
Sous condition d’une distribution normale, 1.96 écarts-type correspond à 2.5 percentiles, ou en arrondissant, - 2 écarts-type au 3ème percentile, et + 2 écarts-type au 97ème percentile. Lorsque sur une courbe (carnet de santé), on dispose de valeurs, pour un âge donné, du 3ème percentile et du 97ème percentile, on peut calculer l’écart-tye.
On peut effectuer une transformation de variables quantitatives en classes (donc qualitatives) : ne jamais le faire a priori dans un questionnaire ++++. On pourra toujours le faire au moment de la présentation des résultats. Exemple à ne pas faire : âge de la mère avec le code (1) < 20 ans ; (2) 20 ans à 35 ans ; (3) > 35 ans → le code (2) représentera 95 % des âges !
Donc ++++ profiter du caractère quantitatif d’une variable pour la saisir comme telle (âge, SA, longueur, poids, valeur sanguine…) → les résultats pourrant être exprimés en moyenne, médiane, ou des seuils ou des classes (groupes) seront déterminés.
2
.
2
.
2
-
Les données sont qualitatives (discontinues, discrètes)
2
.
2
.
2
.
1
-
Valeur centrale : pourcentage
Lorsque l'on calcule un taux, un pourcentage, ou une proportion, on donne le résultat brut. Ce résultat doit toujours être assorti de la notification du dénominateur, c'est-à-dire du nombre d'observations sur lesquelles a été calculé le pourcentage. Il n’est pas indifférent de dire que 30 % des malades sont guéris s’il s’agit d’une étude sur 15 malades, ou sur 1000... Par exemple : dire, à la suite d'une expérience, que " 33 % des souris sont mortes, 33 % des souris sont vivantes, et la troisième s'est échappée", n’a pas grand sens (l'expérience a été faite sur 3 souris !)
2
.
2
.
2
.
2
-
Dispersion
* écart-type de pourcentage :
2/12