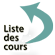3  -  Arrangement structural des solides cristallins

3 . 1  -  Le cristal parfait

Le cristal idéal ou parfait (le cristal réel diffère mais peu) est constitué d’une répartition régulière des atomes, des ions ou des molécules suivant les trois dimensions de l’espace et l’arrangement régulier des atomes s’étend pratiquement à l’infini.

A notre échelle, on a des macrocristaux caractérisés par leur aspect géométrique caractéristique : faces planes, arêtes vives, angles entre les faces bien déterminés (Figure 8).

Un cristal peut être décrit à l’aide d’une entité mathématique, le réseau, et d’un contenu matériel, le motif. « L’assemblage » constitue le cristal.

Figure 8 : Représentation schématique de la structure des macrocristaux d’un métal

3 . 1 . 1  -  Le réseau cristallin

1- Définitions

Le réseau cristallinDéfinitionhttp://fr.wikipedia.org/wiki/Cristallographie.Un réseau est un ensemble de points ou nœuds en trois dimensions qui présente la propriété suivante : lorsque l'on se translate dans l‘espace selon certains vecteurs, on retrouve exactement le même environnement. Il y a donc une périodicité spatiale. Cela permet de définir sept systèmes réticulaires de base : cubique, hexagonal, rhomboèdrique, quadratique (ou tétragonal), orthorhombique, monoclinique, triclinique. est décrit par une entité mathématique de base appelée RESEAU.              

Ce n’est pas un cristal. C’est un ensemble de points qui n’a aucune matérialité.

L’ensemble des points M forme les NOEUDS du réseau, occupés ou non par des particules (Figure 9).

L’origine O est un nœud, donné par p = q = r = 0. Les vecteurs de base ne sont pas uniques pour un réseau donné ; ainsi le réseau plan ci-dessous pourrait bien être défini par les vecteurs de base a et a + b, par exemple. 

Figure 9 : Représentation schématique d’un réseau plan
Le réseau est défini par l’ensemble des points M, ceux-ci formant les nœuds du réseau, occupés ou non par des atomes. La localisation des noeuds est déterminée par un système vectoriel. Une rangée réticulaire est définie par une droite passant par minimum deux nœuds. p est appelé paramètre de la rangée réticulaire et correspond à la distance entre deux nœuds de la rangée réticulaire.

2- Mailles élémentaires

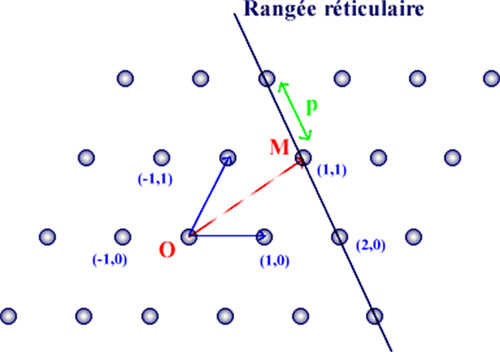
 Maille élémentaire = tout polyèdre ayant pour sommets des nœuds du réseau, et tel que l’empilement de polyèdres tous identiques au premier puisse remplir tout l’espace sans vide ni recouvrements de matière (Figure 10).

Ex : carrelages – la maille élémentaire = petit carreau. 

Pour compter le nombre de nœuds « contenus » dans une maille élémentaire, il faut tenir compte du fait que les sommets du polyèdre appartiennent simultanément à un nombre p de mailles adjacentes ; chacun d’eux comptera donc pour 1 /p nœud. Il est possible de démontrer qu’une maille élémentaire contient toujours un nombre entier N de nœuds.

- Décompte du nombre de nœuds (dans un réseau 3D, tel que dans la réalité) contenus dans une maille élémentaire (toujours un nombre entier) :

Si on considère un cube … On peut compter les particules qui se trouvent dans une maille : (1) si un atome est dans la maille, il y est à 100% et il compte donc pour 1. (2) si l’atome est au centre de la face, une partie est dedans et l’autre est dehors : l’atome compte pour 1/2. (3) si l’atome est centré sur le sommet, il compte pour 1/8 (Il y a 4 cubes au-dessus et 4 cubes au-dessous). (4) si un atome est au centre d’une arête, il compte pour 1/4. (Figure 11). 

Figure 10 : Exemple de mailles élémentaires
(a) rectangle, (b) parallélogramme, (c) hexagone.
Figure 11 : Densité des nœuds du réseau
(1) atome dans la maille (=1), (2) atome au centre de la face (= ½), (3) atome centré sur le sommet de la maille (=1/8), (4) atome au centre d’une arête (=1/4).

3- Types de réseaux cristallins

 Jusqu’à présent, on a parlé du réseau mathématique. On passe maintenant au réseau cristallin.

Il existe 7 systèmes cristallins. Bravais (1848) a montré qu’il y avait en fait 14 systèmes cristallins et tous les cristaux appartiennent à ces systèmes : 

  • Système cubique :           

- Système cubique simple : atomes présents uniquement aux points du réseau.
- Système cubique centré (système CC) : il y a un atome supplémentaire au centre du cube.
- Système cubique faces centrées (système CFC) : chaque face comporte un atome au centre de celle-ci.

  • Système hexagonal : le système hexagonal peut se décomposer en prismes à base losangique.

- Système orthorhombique : simple, à 2 faces centrées, à faces centrées, à prismes centrés.
- Système clinorhombique : simple, à faces centrées
- Système rhomboédrique : 1 seul système
- Système quadratique : simple, centré
- Triclinique : 1 seul système.

Deux de ces systèmes seront exposés ici : le système cubique et le système hexagonal. En effet, la majorité des métaux et des solides utilisés en odontologie cristallisent dans ces deux systèmes. 

3 . 1 . 2  -  Structure cristalline

Le motif constitue le contenu matériel du cristal, par opposition au réseau, entité purement mathématique qui décrit la géométrie de l’édifice cristallin. Les constituants élémentaires du motif peuvent être de différents types, correspondant à différentes catégories de cristaux.

Rappel : les métaux sont constitués d’ions positifs immergés dans un « gaz électroniques », la cohésion de l’ensemble résultant de la liaison métallique. Le gaz d’électrons étant réparti de façon plus ou moins homogène dans le cristal, c’est en fait la répartition des ions positifs, que l’on désignera dans la suite par « atomes » pour simplifier, qui caractérise la structure du cristal métallique.
Dans le réseau (entité mathématique), il peut y avoir des atomes absents des points et des atomes en des points qui ne sont pas des nœuds du réseau.  

Le motif d’un cristal (métallique) est donc les atomes contenus dans une maille élémentaire (à spécifier dans chaque cas), le cristal résultant de la répétition tridimensionnelle de ce motif suivant les translations du réseau associé.

Goldschmidt (1926) a proposé de représenter les atomes sous forme de sphères.
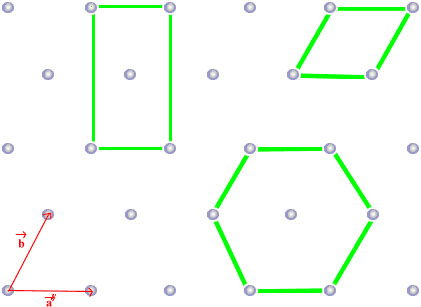
1 - Structure cubique centrée (CC)

Figure 12 : Structure cubique centrée (CC)
(a) maille élémentaire - les points noirs entourés d’un cercle bleu représentent les nœuds du réseau. Les ronds bleus foncés représentent le motif de la maille cubique = atomes (n = 2) - (b) représentation des atomes.

Exemple de métaux : fer α et chrome.

Le réseau = sommet du cube. Ici, tous les nœuds du réseau sont occupés et il y a un atome au centre et cet atome n’est pas au niveau d’un nœud du réseau. Il faut donc bien distinguer le nœud du réseau qui est une entité mathématique et la maille (contient des atomes) qui est une entité matérielle.

La maille élémentaire comporte 2 atomes : 1 au centre du cube et qui donc compte pour 1 et les 8 qui sont au sommet qui comptent pour 1/8 : 8 x 1/8 = 1 + 1 = 2.

2- Structure cubique à faces centrées (CFC)

Figure 13 : Structure cubique faces centrées (CFC)
(a) maille élémentaire - les points noirs entourés d’un cercle bleu représentent les nœuds du réseau. Les ronds bleus foncés représentent le motif de la maille cubique = atomes (n = 4) – (b) Représentation des atomes.

Exemple de métaux : aluminium, cuivre, nickel, fer γ.

La maille élémentaire comporte 4 atomes.

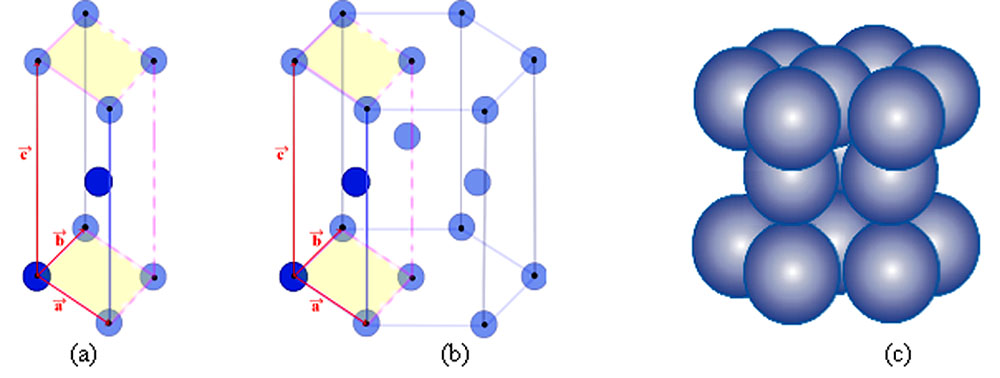
3- Structure hexagonale compacte (HC)

Figure 14 : Structure hexagonale compacte (HC)
(a) maille élémentaire : prisme à base losangique. . Les ronds bleus foncés représentent le motif de la maille hexagonale = atomes (n = 2) – (b) maille de la structure hexagonale compacte (HC) – (c) Représentation des atomes.

Exemple de métaux : zinc, magnésium, zirconium α et le titane α.

Le réseau associé à cette structure est hexagonal et la maille élémentaire utilisée est le prisme droit à base losange. Le motif contenu dans cette maille est constitué de 2 atomes.

4- Empilements des sphères
Certains atomes ne s’empilent pas correctement et cela introduit des défauts (cf. Le cristal réel).

a/ Les deux types d’empilements

Les structures CFC et HC peuvent être présentées d’une autre manière en considérant des empilements de sphères identiques et indéformables, figurant les atomes. Comment disposer ces sphères de façon à obtenir le maximum de compacité (le moins de vide), c’est-à-dire à minimiser le volume de vide entre les sphères ?

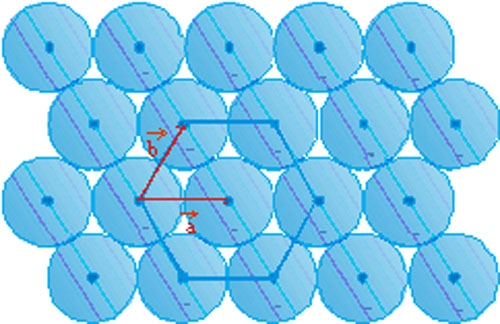
Pour un empilement à une dimension, la solution est simple (Figure 15). Pour un empilement à deux dimensions, il est également facile d’obtenir le résultat (Figure 16).

Figure 15 : Empilement de sphères – 1 dimension
Figure 16 : Empilement de sphères – 2 dimensions

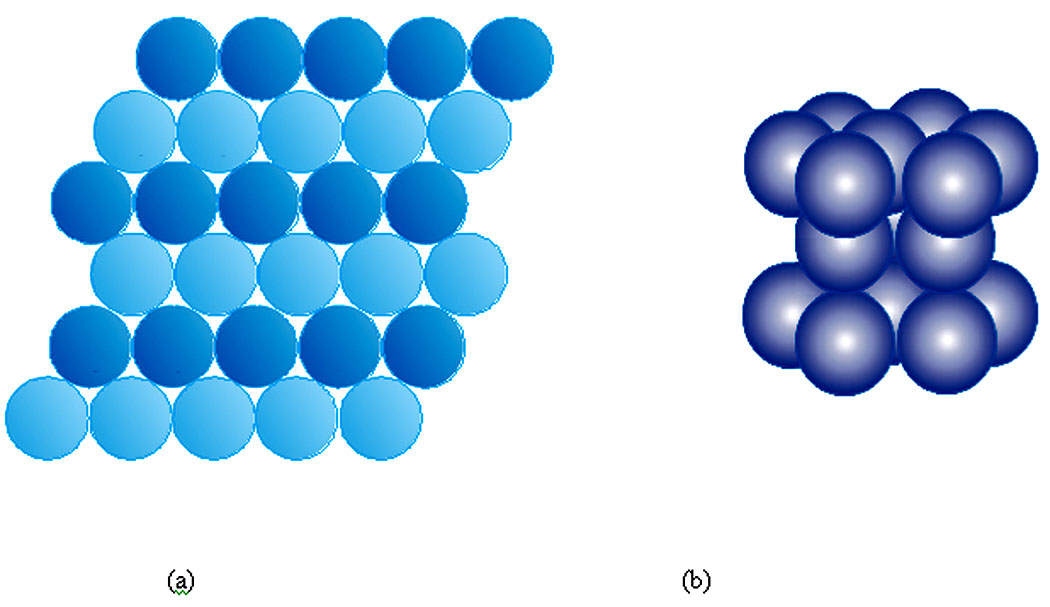
Pour l’empilement en trois dimensions (Figure 17), il faut superposer des plans de 2 dimensions les uns sur lesautres et, pour assurer le maximum de compacité. Il faut translater le plan B de 1 vers 2 sur le plan A. Les centres des atomes du plan B se trouvent alors à l’aplomb des interstices du plan A et les interstices du plan B se trouvent soit à l’aplomb des interstices du plan A, soit à l’aplomb du centre des atomes du plan A. Le plan suivant peut être translaté de 2 façons : de 1 vers 2 et on aura un empilement ABCABC, soit de 2 vers 1 et on aura un empilement ABAB.

Figure 17 : Empilement de sphères (empilement AB)
« 3 dimensions » : empilement AB : (a) vue de « face » - (b) vue de « profil ».

En répétant invariablement l’une ou l’autre de ces deux procédures, on obtient deux types d’empilements : translations 1,2   : ABCABC, translation 1,2 puis 2,1 : ABAB

b/ Dans les structures CFC et HC

 ABCABC correspond à CFC (Figure 19) et ABAB correspond à HC (Figure 18) 

Figure 18 : Empilement ABAB de sphères et structure cristalline correspondante (structure hexagonale compacte HC)
(a) vue en 2 dimensions – (b) vue en 3 dimensions
Figure 19 : Empilement ABCABC de sphères et structure cristalline correspondante (structure cubique à faces centrées CFC)
(a) vue en 2 dimensions – (b) vue en 3 dimensions.
4/10