Cours de chimie UNF3S

La thermodynamique étudie les lois qui gouvernent les échanges d'énergie et de matière d'un système avec le milieu qui l'entoure.

Un système est la partie de l'univers sur lequel porte l'étude thermodynamique. Par convention, toute énergie apportée au système est comptée positivement ; toute énergie cédée par le système est comptée négativement.

Un système peut être décrit grâce à des variables d'état. La masse m, le volume V, les quantités de matière ni, la température T et la pression P sont des exemples de variables d'état.

Certaines de ces variables peuvent être liées entre elles par une relation appelée équation d'état. Un exemple est celui du gaz parfait pour lequel P, V, n et T :

P.V = n.R.T

Grâce à ces relations il n'est donc pas nécessaire de connaître toutes les variables d'état pour décrire complètement un système.

En thermodynamique, on distingue deux types de variables d'état :

Les variables extensives qui sont proportionnelles à la quantité globale de matière du système (exemples : la masse m)

Les variables intensives qui sont indépendantes de la quantité globale de matière du système (exemples : la pression P)

Une fonction d'état est une grandeur extensive qui ne dépend que des variables d'état.

Comme pour les variables d'état, une fonction d'état X est constante pour un état donné du système. Elle possède les propriétés suivantes :

Sa variation, notée , ne dépend que de l'état initial et de l'état final du système :

X = X_final-X_initial

Sa variation est indépendante des transformations qui amènent le système de l'état initial à l'état final. On dit encore qu'elle ne dépend pas du « chemin suivi » pour passer de l'état initial à l'état final.

Le passage d'un système d'un état initial à un état final se fait par une ou plusieurs transformations qui peuvent être de différentes natures. Parmi celles-ci, on trouve :

Les transformations adiabatiques : transformations sans échange de chaleur avec le milieu extérieur.

Les transformations isothermes : transformations à température constante.

Les transformations isobares : transformations à pression constante.

Les transformations isochores : transformations à volume constant.

Lorsque l'on étudie une réaction chimique, il est important de connaître l'état physique des réactifs et des produits car les paramètres thermodynamiques relatifs à ces espèces dépendent de leur état. Pour comparer des données issues de plusieurs réactions, il est nécessaire de définir parmi les différents états possibles de la matière, un état « de référence » appelé état standard.

Pression standard

Les états standards correspondent à une pression dite pression standard, notée P0, et conventionnellement fixée à :

P⁰ = 1 bar = 105 Pa = 0,9872 atm = 750 mm Hg

Contrairement à certaines idées reçues, un état standard ne correspond pas à une température fixée.

État standard d'un constituant

L'état standard d'un constituant est l'état physique de ce corps à la pression standard P0 et à la température T considérée. En thermodynamique, les températures sont exprimées en degré Celsius (°C) ou en Kelvin (K). La correspondance entre ces deux unités est la suivante :

T(K) = T(°C) + 273,15

A chaque température, correspond un état standard particulier. Il est donc nécessaire de préciser la température pour définir l'état standard considéré.

Sous la pression standard et à la température considérée, la substance étudiée peut être dans un état stable (carbone graphite à 298 K) ou non (eau vapeur à 298 K).

État standard de référence d'un constituant

Pour un même composé, il est possible de définir plusieurs états standard à une même température T (eau vapeur à 298 K, eau liquide à 298 K, eau solide à 298 K). Parmi ceux-ci on distingue l'un d'entre eux, appelé état standard de référence.

L'état standard de référence d'un corps pur, à la température T, est l'état standard du corps pur simple à cette température.

Ainsi, pour un corps ou un constituant à une température donnée, il est possible de définir plusieurs états standard mais il n'existe qu'un seul état standard de référence.

Exemple :

A 398 K (125°C), l'état standard de référence de l'eau est H2O_(g).

A 298 K (25°C), l'état standard de référence de l'eau est H2O_(l).

Pour certaines espèces chimiques, l'état standard de référence n'est pas celui dicté par la règle générale :

Pour les éléments, autres que les gaz rares, dont le corps simple a une température d'ébullition, sous 1 bar, inférieure à 25°C, l'état standard de référence de l'élément correspondant est le gaz parfait diatomique sous 1 bar, quelle que soit la température. C'est le cas pour les éléments hydrogène (H₂), azote (N₂), oxygène (O₂), fluor (F₂) et chlore (Cl₂).

Pour le carbone, l'état standard de référence est le carbone graphite à toute température, sous 1 bar.

Énergie interne U

Le premier principe de la thermodynamique est un principe de conservation de l'énergie. Il stipule que la quantité d'énergie dans l'Univers est constante. On peut l'énoncer comme suit :

« L'énergie se conserve, elle ne peut être ni créée, ni détruite »

Pour tout système, il est possible de définir une grandeur extensive, homogène à une énergie, appelée énergie interne et notée U.

Le premier principe postule que la variation d'énergie interne U d'un système au cours d'une transformation

ne dépend que de l'état initial et de l'état final du système : U = U_final-U_initial

est indépendante des transformations qui amènent le système de l'état initial à l'état final.

est égale à la somme des quantités de chaleur Q et de travail W échangées entre le système et le milieu extérieur, soit :

U = U_final-U_initial = W + Q

L'énergie interne U est une fonction d'état alors que le travail W et la chaleur Q ne le sont pas. La quantité de chaleur et le travail échangés dépendront du chemin suivi pour passer d'un état initial à un état final du système.

L'énergie interne, le travail et la chaleur sont exprimés généralement en Joule (J) qui est l'unité standard internationale.

Si la transformation est isochore, le système n'échange donc de l'énergie que sous forme de chaleur. En notant QV, la quantité de chaleur échangée dans une transformation à volume constant, le premier principe s'écrit alors :

U = Q_V

Enthalpie H

Les réactions chimiques ou biochimiques ont lieu le plus souvent à pression constante. On définit alors une autre grandeur extensive, la fonction d'état appelée enthalpie, notée H et exprimée également en Joule, qui est plus spécialement adaptée aux transformations à pression constante :

H = U + PV

Transformation à pression constante

Si la transformation est isobare (transformation à pression constante), la quantité de chaleur échangée QP au cours de cette transformation est égale à la variation d'enthalpie du système :

H = Q_P

Relation entre U et H pour des transformations isothermes.

Pour un système qui évolue d'un état initial i à un état final f, on peut écrire la variation de son enthalpie comme suit :

H = H_f - H_i = (U+PV) = U + (PV)

On peut réécrire l'expression ci-dessus en considérant que seuls les gaz sont compressibles :

H=U+(PV)_gaz

Dans le cas d'une transformation isotherme et en considérant les gaz comme parfaits, l'expression précédente devient :

H=U+RT.n_gaz

n_gaz représente la variation du nombre de moles gazeuses au cours de la transformation.

Lorsque le système étudié ne contient pas de composés gazeux, où si n_gaz = 0 lors de la transformation, alors H = U.

Capacités calorifiques

Expérimentalement, on montre qu'un corps pur homogène qui subit une variation de température T, sans changer de phase, perd ou reçoit une quantité de chaleur proportionnelle à sa masse m (ou à son nombre de moles n) et à la variation de température :

Pour une transformation à pression constante :

Q_P = m.c_P.T = n.C_P.T

c_P est la capacité calorifique massique à pression constante, exprimée en J.kg^-1.K^-1.

C_P est la capacité calorifique molaire à pression constante, exprimée en J.mol^-1.K^-1.

Pour une transformation à volume constant :

QV = m.c_V.T = n.C_V.T

c_V est la capacité calorifique massique à volume constant ; C_V la capacité calorifique molaire à volume constant. Leurs unités sont les mêmes que celles des capacités calorifiques à pression constante.

Les capacités calorifiques massiques (resp. molaires) désignent les quantités de chaleur nécessaires à apporter à un kilogramme (resp. une mole) d'un corps pur à pression constante ou volume constant, pour augmenter sa température de 1 K.

Cas du gaz parfait

Joule a montré que l'énergie interne et l'enthalpie d'un gaz parfait ne dépendent que de la température, même si la transformation n'a pas lieu à volume constant ou pression constante.

On peut alors écrire :

H = n.C_P.T

U = n.C_V.T

Cas des phases condensées

Pour une phase condensée liquide ou solide, l'influence d'une variation de pression ou de volume sur l'énergie interne ou l'enthalpie est souvent négligeable. Le système ne contenant pas de gaz, ces deux énergies sont sensiblement égales comme nous l'avons montré précédemment. On peut donc écrire :

H = U = n.C.T

La thermochimie est le domaine de la chimie qui étudie les échanges d'énergie qui accompagnent les réactions chimiques. Les énergies mises en jeu sont la chaleur et le travail des forces de pression (ou travail mécanique).

Chaleur de réaction isotherme

La chaleur de réaction Q_R est la quantité de chaleur reçue ou cédée par un système au cours d'un avancement  de la réaction à une température T. En laboratoire, les réactions ont lieu le plus souvent à pression atmosphérique constante (assimilée à la pression standard P). Dans ce cas, la chaleur de réaction est égale à l'enthalpie standard de réaction (notée _rH) :

Q_RP = _rH⁰

Si _rH⁰ > 0, alors la réaction est dite endothermique. Elle absorbe de la chaleur.

Si _rH⁰ < 0, alors la réaction est dite exothermique. Elle cède de la chaleur.

Si _rH⁰ = 0, alors la réaction est dite athermique. Elle n'échange pas de chaleur.

Les grandeurs standard de réaction sont tabulées à une température bien précise, 298 K. Toutes les réactions n'ayant pas lieu à cette température, il est nécessaire de pouvoir déterminer la valeur d'une grandeur standard de réaction à n'importe quelle température.

Les lois de Kirchhoff sont utilisées sous leur forme intégrée. Pour l'enthalpie standard de réaction, la forme intégrée s'écrit :

Loi de Hess

L'enthalpie H étant une fonction d'état, l'enthalpie standard de réaction _rH⁰ est indépendante du chemin suivi au cours d'une transformation et ne dépend donc que de l'état initial et de l'état final.

Dans certains cas, l'enthalpie standard d'une réaction n'est pas calculable. Pour la déterminer on va établir un cycle thermodynamique grâce auquel on pourra calculer l'enthalpie standard de réaction en suivant une autre voie fictive ou non.

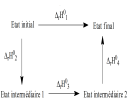
Pour déterminer la grandeur inconnue _rH₁⁰pour la réaction étudiée, on établira un cycle thermodynamique comme celui représenté ci-dessous. Pour aller de l'état initial à l'état final, on peut envisager un chemin passant par deux états intermédiaires. Pour ce chemin les enthalpies standard de réaction sont connues. Le premier principe permet alors d'écrire :

_rH₁⁰ = _rH₂⁰ +_rH₃⁰ +_rH₄⁰

Réaction standard de formation d'une espèce chimique

Par définition, la réaction standard de formation d'une espèce chimique, à une température T et dans un état physique donné, est la réaction au cours de laquelle une mole de cette espèce, dans son état standard, est formée à partir des corps simples correspondants aux éléments qui le constituent; chacun des corps simples devant se trouver dans son état standard de référence à la température T.

Enthalpie standard de formation d'une espèce chimique

L'enthalpie standard de formation d'une espèce chimique X est l'enthalpie standard de la réaction standard de formation de cette espèce (la réaction de formation d'une mole de cette espèce à partir de ses éléments pris dans leur état standard de référence, à la température T) à une température T et dans un état physique donné.

Cette grandeur est notée _fH⁰, l'indice f faisant référence à la formation.

D'après cette définition, l'enthalpie standard de formation d'un corps simple correspondant à l'état standard de référence de l'élément (H2, O2, C(s)) est nulle.

Selon cette définition _fH⁰ (C graphite) = 0 ; _fH⁰ (O₂ gaz) = 0 ; _fH⁰ (H₂ gaz) = 0

Cas d'une molécule diatomique

Par convention, l'énergie de liaison d'une molécule diatomique AB, notée DA–B, correspond à la variation d'énergie interne standard qui accompagne la réaction au cours de laquelle une mole de AB à l'état gazeux est dissociée, à 0 K, en deux radicaux à l'état gazeux selon la réaction :

A–B(g) = A^._(g) + B^._(g)

L'énergie de liaison est toujours une valeur positive car elle correspond à l'énergie qu'il faut fournir pour casser une liaison.

Par souci de simplification, on suppose que l'énergie de liaison est indépendante de l'environnement de la liaison étudiée. L'énergie donnée dans les tables, à 298 K, est une valeur moyenne des énergies de dissociation de cette liaison, déterminées sur un ensemble de composés possédant cette liaison.

Quelques défnitions supplémentaires :

Definition :

Le premier principe, qui est un principe de conservation, permet de déterminer l'énergie échangée par une réaction lorsque celle-ci a lieu à pression ou volume constant. Toutefois, ce principe ne nous indique pas si la réaction étudiée est spontanée ou non. Pour étudier l'évolution d'une réaction, il faut faire appel au second principe de la thermodynamique (principe d'évolution).

Le second principe se base sur une nouvelle fonction d'état extensive, l'entropie S, pour déterminer si une transformation est spontanée ou non.

De la définition donnée de l'entropie découlent plusieurs propriétés :

• Pour un système isolé (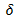Q = 0) qui évolue réversiblement : 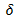S = 0

• Un système isolé qui évolue de manière irréversible voit son entropie augmenter. Ainsi l'entropie de l'univers augmente continuellement !

Le deuxième principe fournit donc bien un critère d'évolution des transformations dans le cas des systèmes isolés : si S > 0 la transformation est spontanée, si S = 0 le système est en équilibre (transformation réversible passant par une infinité d'états d'équilibre).

Entropie absolue d'un corps pur

La thermodynamique statistique montre que l'entropie d'un corps pur, parfaitement cristallin, au zéro absolu (T = 0 K) est nulle. Ceci constitue le troisième principe de la thermodynamique :

S_cr (0 K) = 0

Application aux réactions chimiques

Le classement suivant peut etre établit :

S_solide < S_liquide < S_gaz

l'entropie molaire standard absolue est plus élevée dans le cas d'une espèce gazeuse pour laquelle le désordre dû à l'agitation thermique est plus important.

Pour prévoir l'évolution d'un système non isolé, il faut utiliser une nouvelle fonction d'état extensive : l'enthalpie libre G dans le cas d'une transformation à P et T constants ou l'énergie libre F dans le cas d'une transformation à T et V constants. Par définition :

G = H – TS

F = U – TS

Les transformations spontanées ayant lieu le plus souvent à pression constante, on privilégiera l'emploi de l'enthalpie libre G. La variation d'enthalpie libre lors d'une réaction s'écrit alors :

G = H – (TS) = U + (PV) – (TS)

Pour une transformation à température et pression constantes et dans le cas où seul le travail des forces de pression intervient (W = - P_ext.V) :

G = Q – T.S

Pour une transformation spontanée à T constante, la condition d'évolution spontanée d'un système, à P et T constantes est :

G < 0

De la même manière que nous avons défini les enthalpies molaires standard de réaction, on peut également définir des enthalpies libres molaires standard de réaction :

_rG⁰ = _rH⁰ – T._rS⁰

On peut appliquer la loi de Hess pour l'enthalpie libre, comme on le fait pour l'enthalpie.

Dans ces conditions, le critère d'évolution d'une réaction est _rG⁰ < 0. Lorsque la réaction n'évolue plus alors _rG⁰ = 0.