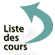- Pré-requis et Objectifs
-
Cours
-
Contenu
- 1 - Contraintes et déformations
- 2 - Caractérisation des propriétés mécaniques
-
3 - L’essai de traction simple
- 3.1 - Diagramme contrainte-déformation en traction d’une éprouvette en métal
- 3.2 - Comportement macroscopique d’une éprouvette en métal en traction simple
- 3.3 - Comportement microscopique de l’éprouvette en métal en traction simple
- 3.4 - Diagramme contrainte-déformation en traction des différents matériaux
- 4 - Les essais de compression et flexion
- 5 - Essai de cisaillement
- 6 - Essais de dureté
- 7 - Rupture Fragile. Essai de résilience
- 8 - Essais de fatigue
- 9 - Essais de fluage
-
Version PDF

-
Contenu
- Annexes
3 - L’essai de traction simple
L'essai le plus fréquemment utilisé afin de déterminer le comportement mécanique d'un matériau est l'essai de traction. Cet essai est caractérisé par sa facilité de mise en œuvre et par la richesse des informations fournies.
On exerce une force de traction sur un barreau de dimension standardisée, jusqu'à sa rupture, en suivant un processus de mise en charge à une vitesse de déformation constante.
L’éprouvette d'essai est prélevée dans le matériau à caractériser et usinée à des dimensions normalisées, afin d'assurer une meilleure comparaison des essais effectués dans différents laboratoires. Pour chaque type de matériau, il existe un type d’éprouvette.
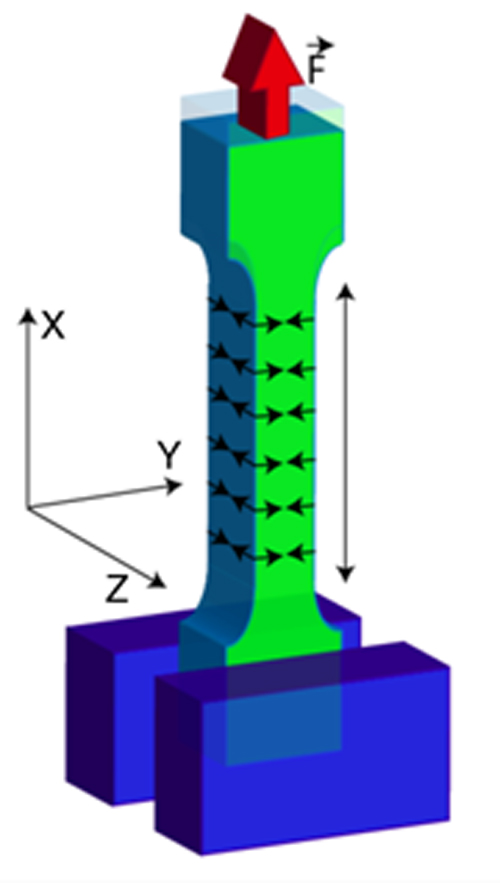
Figure 1. Eprouvette. Machine de traction. Courbe contrainte-déformation
En enregistrant la force appliquée à l'éprouvette par la machine de traction et son allongement progressif on obtient un diagramme contrainte-déformation.
3 . 1 - Diagramme contrainte-déformation en traction d’une éprouvette en métal
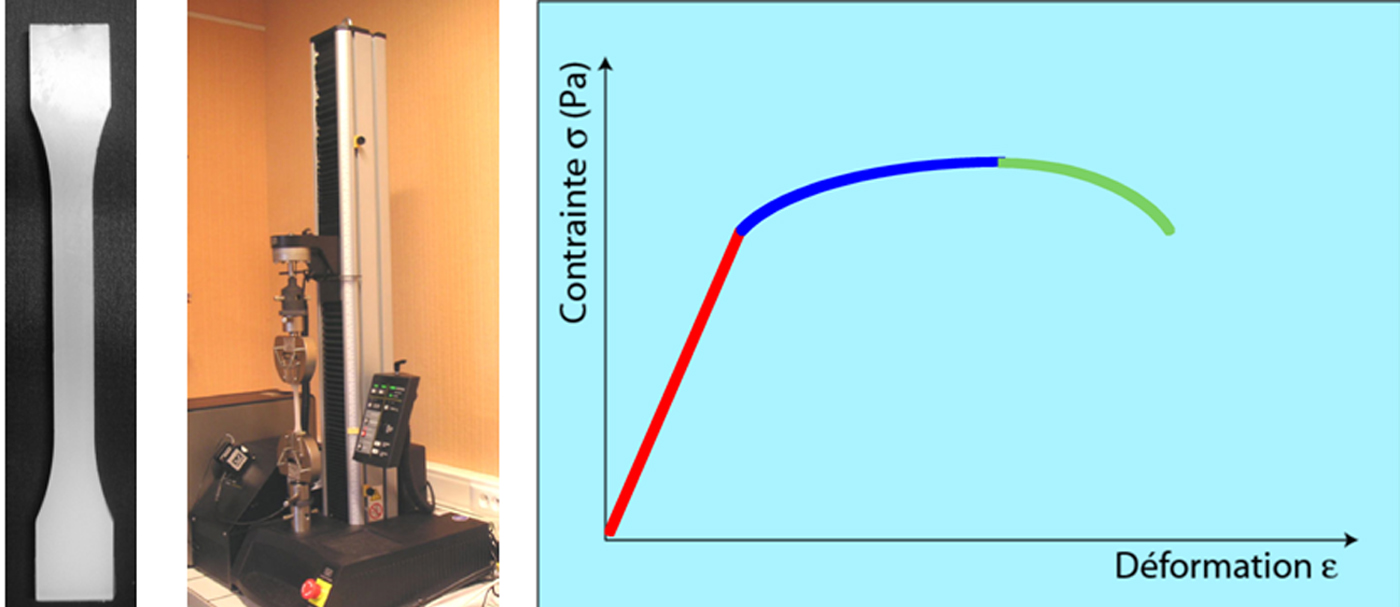
L'application d'une force provoque initialement une déformation élastique de l’éprouvette. Cela se traduit sur le diagramme par une droite car la déformation est proportionnelle, pour un métal, à la contrainte (loi de HOOKE).
Cette déformation élastique est réversible. Si la contrainte est annulée, l’éprouvette revient instantanément à sa forme initiale. Cette déformation élastique est suivie d'une déformation irréversible (permanente) appelée déformation plastique, qui se traduit sur le diagramme par une courbe qui se termine au moment de la rupture de l’éprouvette.
Différents paramètres sont remarquables :
- Le module d'élasticité E (ou module de YOUNG) donné par la pente du domaine élastique du diagramme contrainte-déformation.
⇒⇒ Le module d’élasticité :
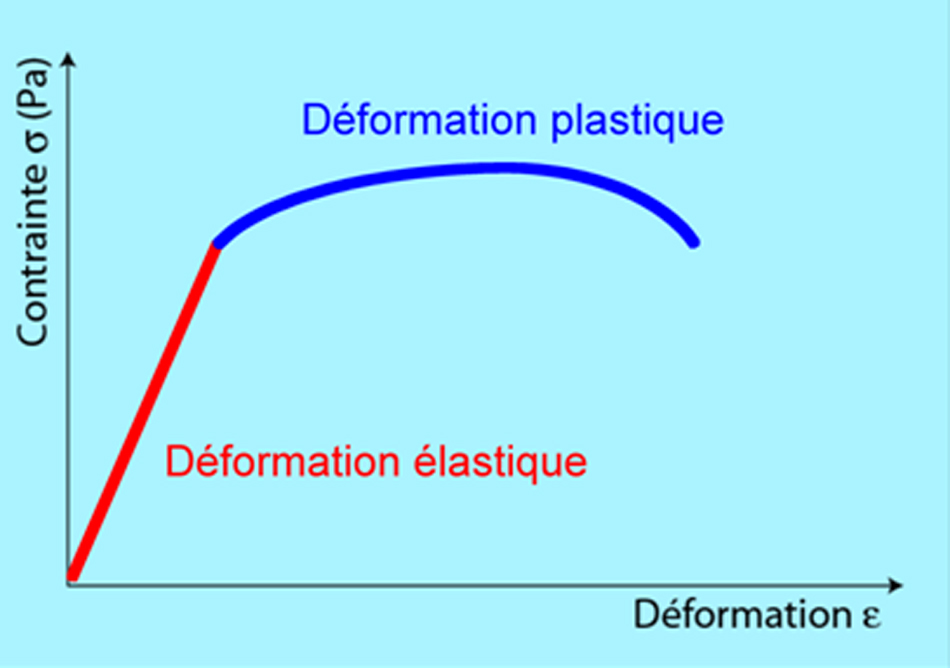
Si l’on raisonne, par simplification, sur un corps parallélépipédique supposé à une seule dimension dans un essai de traction dans un seul axe (uniaxiale, selon l’axe des x), l’éprouvette subit un
allongement (figure 3). Pour les petites déformations, il existe une relation linéaire entre la contrainte et la déformation :
σx = E.εx = E ΔL/L0= E (L- L0)/ L0
E est le module d’élasticité ou module de YOUNG
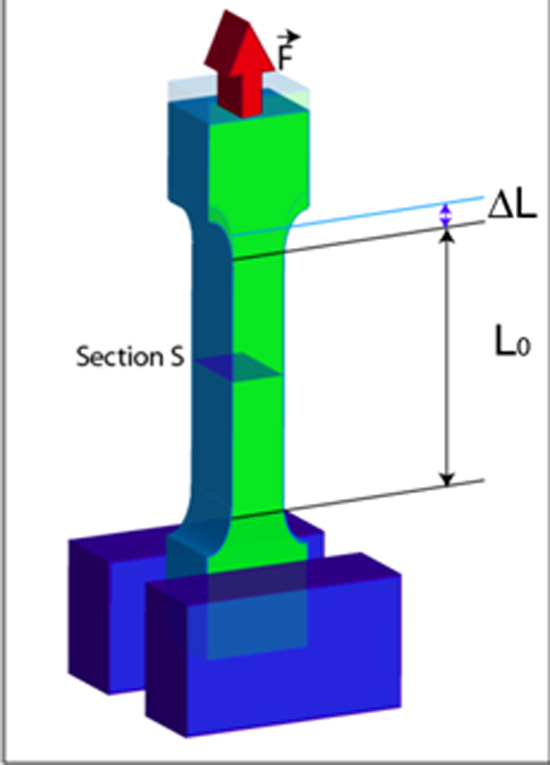
⇒ ⇒ En réalité, l’éprouvette se déforme dans les 3 directions (figure 4).
Dans le sens Ox il y a un allongement, dans les sens Oy et Oz il y a raccourcissement. Dans ce cas de traction simple, si les contraintes σy et σz sont nulles, les déformations εy et εz ne le sont pas. Les 3
déformations sont reliées par le coefficient de POISSON.
εx = -εy/v= - εz/v
v
est le coefficient de POISSON
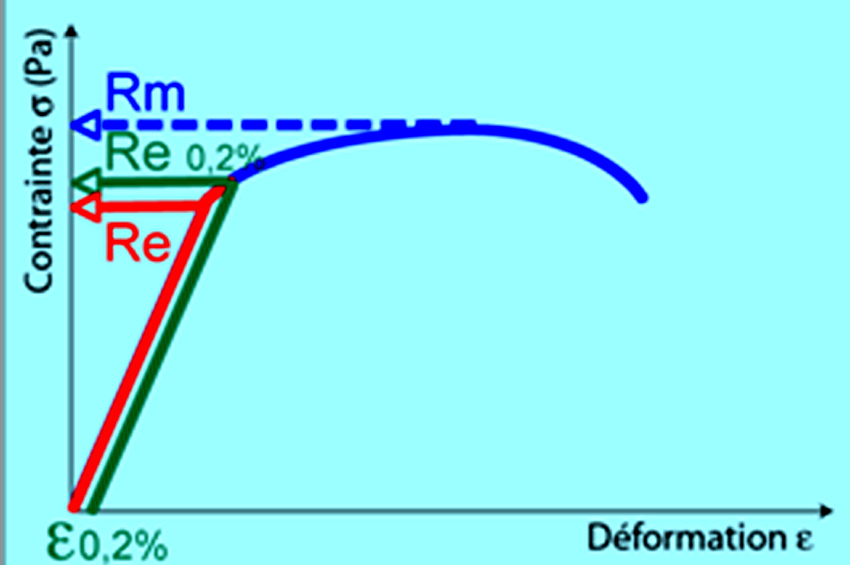
- La limite d'élasticité Re correspond à la contrainte à partir de laquelle le matériau commence à se déformer plastiquement. En pratique, bien que la définition soit simple, cette limite est difficile à apprécier car le passage du domaine élastique au domaine plastique se fait de façon progressive. La difficulté de lecture donnerait des interprétations erronées de cette limite d’un laboratoire à l’autre. Pour s’en affranchir, on a déterminé une limite conventionnelle d’élasticité à 0,2% (Re 0,2%). C’est la contrainte pour laquelle on mesure une déformation plastique de 0,2%.
- La résistance à la traction Rm se définit comme la contrainte maximale atteinte durant l’essai de traction.
- L’allongement à la rupture
εr que l’on peut lire sur le diagramme ou sur l’éprouvette rompue.
On peut également définir certaines caractéristiques déterminées par l'essai de traction :
- la rigidité est fonction de l'énergie des liaisons entre les atomes ou les molécules constituant le matériau. On mesure la rigidité principalement par le module d’YOUNG. Plus ce module est élevé, plus le matériau est rigide.
- la résistance caractérise la contrainte maximale qu’un matériau supporte avant de se rompre. Cette résistance est fonction de l’intensité des liaisons mais également de la forme des pièces ou de ses défauts.
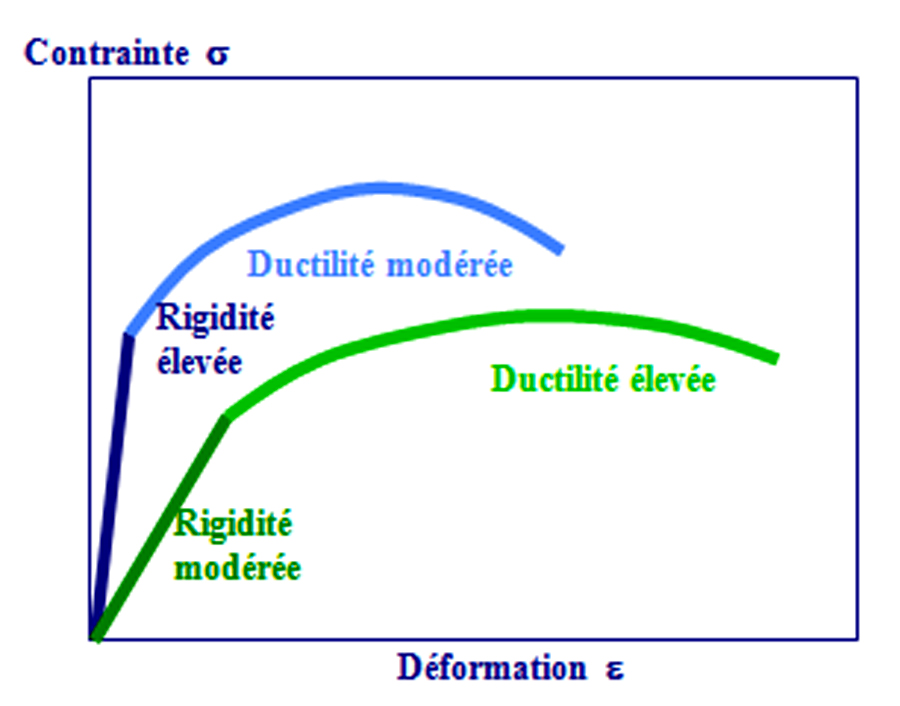
- la ductilité correspond à la capacité d’un matériau à se déformer de façon permanente avant de se rompre. Plus l’allongement à la rupture est élevé, plus le matériau est considéré comme ductile. A l’opposé, lorsque la déformation permanent est très réduite ou nulle, on parle d’un matériau fragile. Un matériau fragile peut présenter une résistance très élevée (figure 6).
Figure 6. Courbe contrainte-déformation. Deux matériaux avec des rigidités et des ductilités différentes
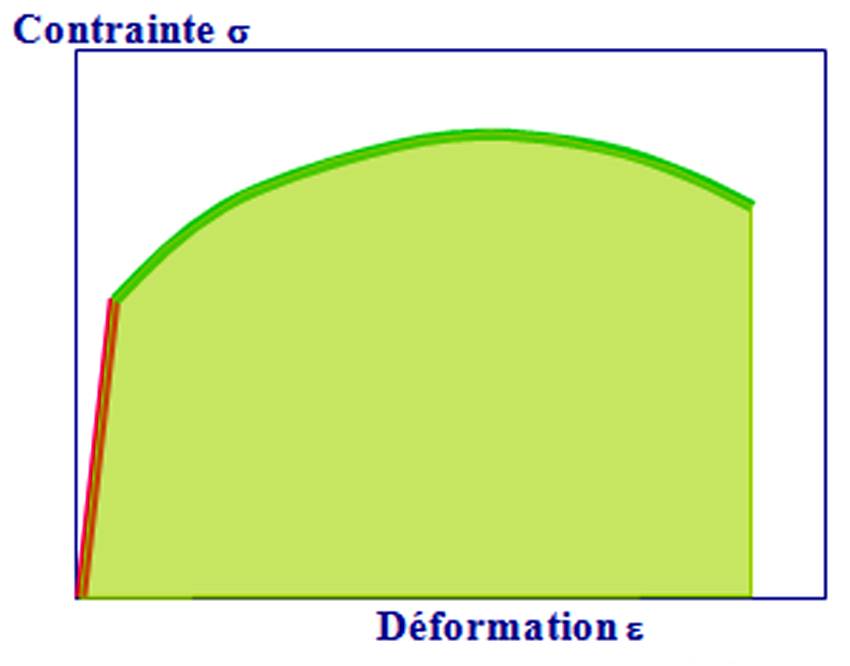
- la ténacité qui représente la quantité d'énergie absorbée à la rupture par un matériau. Elle caractérise la résistance à la propagation brutale de fissures. Sa valeur est égale à l’aire de la surface sous la courbe contrainte-déformation. Cette caractéristique est importante pour les céramiques.
3/12