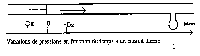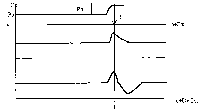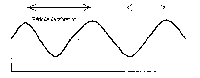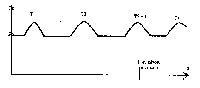
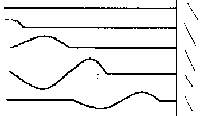
2ème exemple : déformation transverse :
La déformation est de type transverse car la direction de celle-ci est perpendiculaire au sens d'application. Elle se propage de façon linéaire en s'atténuant.
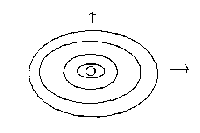
3ème exemple : onde à la surface d'un liquide (milieu 2D) :
La déformation est transverse et se propage de façon circulaire et symétrique en s'atténuant.
4ème exemple : baguette vibrant dans l'eau :
La déformation longitudinale se propage de façon plane en s'atténuant ; de plus, la direction de déformation du milieu est parallèle à celle de la propagation et tous les points d'un même signal s'alignent sur un même plan.
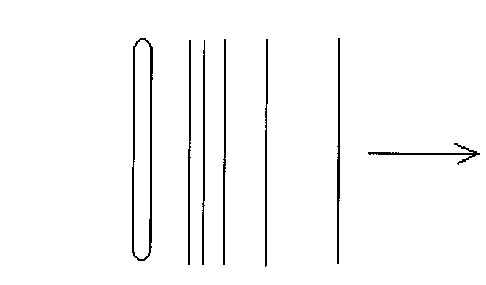
5ème exemple : onde sonore dans l'espace (milieu 3D) :
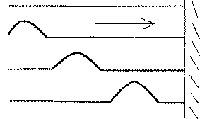
La
déformation longitudinale se propage de façon sphérique
en s'atténuant.
Ces exemples
font apparaître les notions suivantes:
L'excitation du milieu est :
- impulsionnelle, très brève,
- ou bien limitée dans le temps,
- ou continue dans le temps,
- la réponse du milieu propre à celui-ci est une déforination linéaire, plane, cylindrique ou sphérique, transverse ou longitudinale qui se propage en s'atténuant,
- les différentes formes d'excitation utilisées en écho sont :
¤ impulsionnelle : utilisée en écho,
¤ continue : doppler continu,
¤ limitée : doppler pulsé.